CBO: (closed) range predicate cardinality

Now we'll repeat the same steps we made for (bounded, open) ranges, but changing the template to

select x from t where x >= low_x and x <= low_x + w

i.e. we'll move to the (bounded, closed) case.

Selection over an infinitesimal range

The "infinitesimal" range case is covered by the script range_sel_closed_inf.sql, which produces the red (num_distinct=2), green (num_distinct=3) and blue (num_distinct=4) line data for this graph:

Deductions (again, the ones labeled by [JLB] are already discussed in Jonathan Lewis' Book "Cost Based Oracle"):

The specular simmetry around the midinterval point 5.0 = (max_x - min_x) / 2 holds for this case also [JLB];
There's the same flat region at the center, surrounded by the same two lateral bands (ramps) whose width is B = (max_x - min_x) / num_distinct [JLB];
For ranges completely contained in the central flat region, the cardinality honours the standard formula, that for closed ranges has to be modified to (changes underlined):
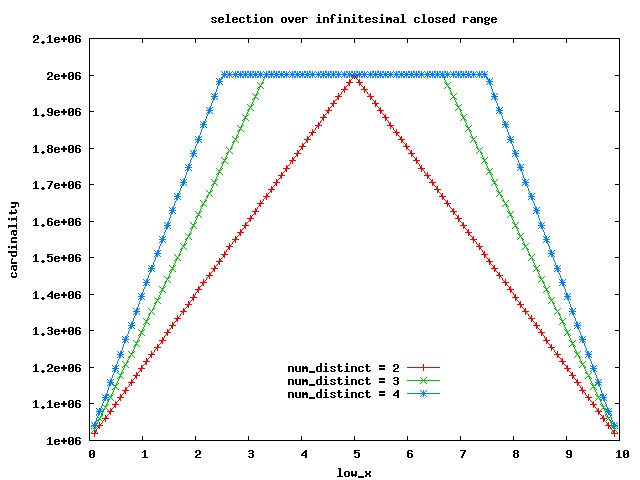
```
 cardinality = num_rows * w / (max_x - min_x) + 2 * num_rows / num_distinct
 
```
[JLB]

For ranges completely contained in the lateral bands:

the cardinality does not depend on w but depends only on the value of high_x = low_x + w for the left ramp
(and for symmetry, of low_x for the right ramp). Note that in the case of open ranges, it depended on low_x, not high_x (and high_x for the right ramp); the role of range extremata has swapped.

In fact (for num_distinct=4):

 SQL> select x from t where x >= 2 - 0.001 and x <= 2;
 --------------------------------------------------------------------------
 | Id  | Operation         | Name | Rows  | Bytes | Cost (%CPU)| Time     |
 --------------------------------------------------------------------------
 |   0 | SELECT STATEMENT  |      |  1800K|  5273K|  1439   (6)| 00:00:18 |
 |*  1 |  TABLE ACCESS FULL| T    |  1800K|  5273K|  1439   (6)| 00:00:18 |
 --------------------------------------------------------------------------

 SQL> select x from t where x >= 2 - 2     and x <= 2;
 --------------------------------------------------------------------------
 | Id  | Operation         | Name | Rows  | Bytes | Cost (%CPU)| Time     |
 --------------------------------------------------------------------------
 |   0 | SELECT STATEMENT  |      |  1800K|  5273K|  1439   (6)| 00:00:18 |
 |*  1 |  TABLE ACCESS FULL| T    |  1800K|  5273K|  1439   (6)| 00:00:18 |
 --------------------------------------------------------------------------

the cardinality formula (for the left ramp) is (changes underlined):

 let B  = (max_x - min_x) / num_distinct
 let height_ramp = num_rows / num_distinct 
 cardinality = height_ramp  +  height_ramp * (high_x - min_x) / B
 
 Eg for num_distinct=4: B = 2.5; height_ramp = 1,000,000
 for low_x = 1.765830 => cardinality = 1000000 + 1000000 * (1.765830+0.001-0) / 2.5 = 1706732
 which is exactly the value we observe in the blue line data.

low_x = min_x (or high_x = max_x for the right ramp) is not a special case [JLB] (i.e. we don't always get 1 as in the open range case):

 SQL> select x from t where x >= 0 and x <= 2.123;
 --------------------------------------------------------------------------
 | Id  | Operation         | Name | Rows  | Bytes | Cost (%CPU)| Time     |
 --------------------------------------------------------------------------
 |   0 | SELECT STATEMENT  |      |  1849K|  5417K|  1439   (6)| 00:00:18 |
 |*  1 |  TABLE ACCESS FULL| T    |  1849K|  5417K|  1439   (6)| 00:00:18 |
 --------------------------------------------------------------------------
 SQL> select x from t where x >= 2 and x <= 2.123;
 --------------------------------------------------------------------------
 | Id  | Operation         | Name | Rows  | Bytes | Cost (%CPU)| Time     |
 --------------------------------------------------------------------------
 |   0 | SELECT STATEMENT  |      |  1849K|  5417K|  1439   (6)| 00:00:18 |
 |*  1 |  TABLE ACCESS FULL| T    |  1849K|  5417K|  1439   (6)| 00:00:18 |
 --------------------------------------------------------------------------
 Note how the value of low_x is ignored, even if it is equal to 0 (min_x).

For ranges overlapping the regions - check the next section.

Selection over a finite range

The script range_sel_closed_finite.sql repeats the same steps for the open range case (fixed low_x = 0.1, high_x changing over the interval iterating over the same values), of course closing the range:

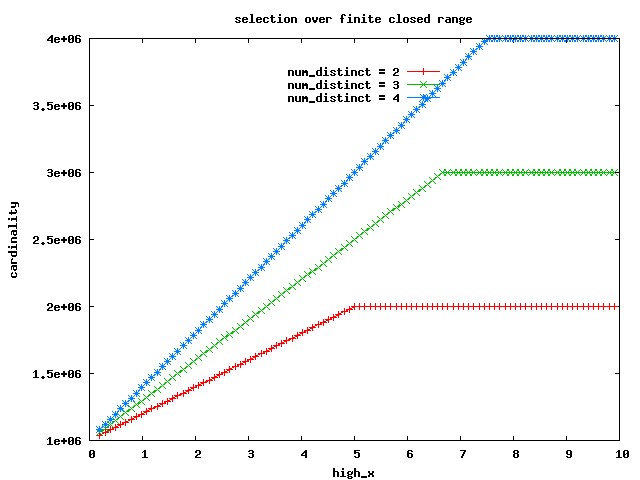
select x from t where x >= low_x and x <= high_x

The usual diagram (click to get the data sets for the red, green and blue line) is:

Deductions:

No flat region on the left for high_x <= min_x + B, since the cardinality depends on high_x, not on low_x, as already observed;

As soon as high_x crosses the min_x + B boundary, the "formal method of ranges decomposition" can be applied, now reformulated (generalised) as (1) break the interval in subintervals, (2)compute the cardinalities over the subintervals, (3)add them, and (3)subtract num_rows/num_distinct for every "<=" or ">=" operator added to break the original interval".

Ie (for num_distinct=4, min_x + B = 2.5):

 SQL> select x from t where x >= 0.1 and x <= 7;
 --------------------------------------------------------------------------
 | Id  | Operation         | Name | Rows  | Bytes | Cost (%CPU)| Time     |
 --------------------------------------------------------------------------
 |   0 | SELECT STATEMENT  |      |  3800K|    10M|  1448   (7)| 00:00:18 | (ORIGINAL)
 |*  1 |  TABLE ACCESS FULL| T    |  3800K|    10M|  1448   (7)| 00:00:18 |
 --------------------------------------------------------------------------
 SQL> select x from t where x >= 0.1 and x <= 2.5;
 --------------------------------------------------------------------------
 | Id  | Operation         | Name | Rows  | Bytes | Cost (%CPU)| Time     |
 --------------------------------------------------------------------------
 |   0 | SELECT STATEMENT  |      |  2000K|  5859K|  1440   (6)| 00:00:18 | (LEFT BAND)
 |*  1 |  TABLE ACCESS FULL| T    |  2000K|  5859K|  1440   (6)| 00:00:18 |
 --------------------------------------------------------------------------
 SQL> select x from t where x <= 2.5 and x <= 7;
 --------------------------------------------------------------------------
 | Id  | Operation         | Name | Rows  | Bytes | Cost (%CPU)| Time     |
 --------------------------------------------------------------------------
 |   0 | SELECT STATEMENT  |      |  3800K|    10M|  1448   (7)| 00:00:18 | (CENTRAL)
 |*  1 |  TABLE ACCESS FULL| T    |  3800K|    10M|  1448   (7)| 00:00:18 |
 --------------------------------------------------------------------------

 We've added the 2 "<= or >=" operators shown underlined, so:
 2000K + 3800K - 2 * 1000K = 3800K, as requested.

The same applies when high_x enters the "right band" region (we have three ranges now to add of course); again for num_distinct=4:

SQL> select x from t where x >= 0.1 and x <= 9;
--------------------------------------------------------------------------
| Id  | Operation         | Name | Rows  | Bytes | Cost (%CPU)| Time     |
--------------------------------------------------------------------------
|   0 | SELECT STATEMENT  |      |  4000K|    11M|  1449   (7)| 00:00:18 | (ORIGINAL)
|*  1 |  TABLE ACCESS FULL| T    |  4000K|    11M|  1449   (7)| 00:00:18 |
--------------------------------------------------------------------------
SQL> select x from t where x >= 0.1 and x <= 2.5;
--------------------------------------------------------------------------
| Id  | Operation         | Name | Rows  | Bytes | Cost (%CPU)| Time     |
--------------------------------------------------------------------------
|   0 | SELECT STATEMENT  |      |  2000K|  5859K|  1440   (6)| 00:00:18 | (LEFT BAND)
|*  1 |  TABLE ACCESS FULL| T    |  2000K|  5859K|  1440   (6)| 00:00:18 |
--------------------------------------------------------------------------
SQL> select x from t where x <= 2.5 and x <= 7.5;
--------------------------------------------------------------------------
| Id  | Operation         | Name | Rows  | Bytes | Cost (%CPU)| Time     |
--------------------------------------------------------------------------
|   0 | SELECT STATEMENT  |      |  4000K|    11M|  1449   (7)| 00:00:18 | (CENTRAL)
|*  1 |  TABLE ACCESS FULL| T    |  4000K|    11M|  1449   (7)| 00:00:18 |
--------------------------------------------------------------------------
SQL> select x from t where x <= 7.5 and x <= 9;
--------------------------------------------------------------------------
| Id  | Operation         | Name | Rows  | Bytes | Cost (%CPU)| Time     |
--------------------------------------------------------------------------
|   0 | SELECT STATEMENT  |      |  2000K|  5859K|  1440   (6)| 00:00:18 | (RIGHT BAND)
|*  1 |  TABLE ACCESS FULL| T    |  2000K|  5859K|  1440   (6)| 00:00:18 |
--------------------------------------------------------------------------
We've added the 4 "<= or >=" operators shown underlined, so:
2000K + 4000K + 2000K - 4 * 1000K = 4000K, as requested.

NB Equivalently, one could say that the range is considered "chopped at the central region border(s)" (the part of it extending over the bands is ignored) - (ORIGINAL) and (CENTRAL) being the same. But the method can be applied in general also to semi-open, semi-closed ranges, as we'll see.

The standard formula does not apply, not even close (check the column CARD_STND_F in the three data sets), so whenever one of the extremes of the range falls inside one of the two bands, you cannot count on it anymore.

Let's move to the semi-closed, semi-open range case.

For corrections / feedback:
[email protected]